Turnierpoker ist statistisch gesehen praktisch ein Glücksspiel. Dieser etwas längere Artikel soll diese Aussage mathematisch prüfen und Pokerergebnisse mit Schach und Fußball vergleichen.
Nachdem ich im vorigen Teil dieser Serie unter anderem zeigte, dass komplett zufällige Poker-Ergebnisse ganz natürlich aussehen können, will ich in diesem Teil die Ergebnisse tatsächlicher Poker-Turniere auswerten und prüfen, inwieweit diese zufällig aussehen oder Rückschlüsse auf eine ausgeprägte Geschicklichkeitskomponente zulassen.
Dieser Artikel wird zeigen, dass die Ergebnisse einzelner Pokerturniere im höchsten Maß zufällig sind, wenn man sie statistisch betrachtet. Über die sogenannte Rangkorrelation wird diese Zufälligkeit statistisch quantifiziert und mit Schach- und Fußballturnieren verglichen.
Vorweg sei angemerkt, dass sich die Betrachtung in diesem Artikel auf eine überschaubare Anzahl von Turnieren beschränkt. Die getroffenen Aussagen hinsichtlich Poker sind in erster Linie für Live-Turnier-Spieler, die nicht mehr als hundert relevante Turniere pro Jahr spielen, zutreffend. Für Spieler, die online mehrere tausend Turniere spielen, greift die Statistik sehr wahrscheinlich nicht mehr.
Was ist ein Rangkorrelationskoeffizient überhaupt?
Um nachvollziehen zu können, was ich im Folgenden überhaupt betrachte, muss ich einen kleine Einführung zu Korrelationskoeffizienten vorweg bringen.
Generell ist ein Korrelationskoeffizient ist ein Maß in der Statistik, welches angibt, wie stark zwei Messgrößen voneinander abhängen. Er nimmt Werte zwischen -1 und +1 an.
Ein Korrelationskoeffizient von +1 entspricht einer direkten proportionalen Korrelation. Wenn sich zum Beispiel die eine Messgröße verdoppelt, muss sich auch die andere verdoppeln.
Ein Korrelationskoeffizient von -1 entspricht einem antiproportionalen Verhältnis – verdoppelt sich die eine Größe, halbiert sich die andere.
Ein Korrelationskoeffizient von 0 sagt aus, dass die beiden Messgrößen statistisch gar nicht korrelieren, das heißt, dass vom Verhalten der einen Größe keine Rückschlüsse auf das Verhalten der anderen Größe gezogen werden können.
Der Rangkorrelationskoeffizient (RKK) ist eine spezielle Form des Korrelationskoeffizienten, der nicht die Messgrößen selbst vergleicht, sondern die Ränge, welche die einzelnen Werte der beiden Reihen einnehmen.
Ganz einfach formuliert, haben verschiedene Rangkorrelationskoeffizienten zwischen zwei Messgrößen folgende Bedeutungen.
| Rangkorrelationskoeffizient | Bedeutung |
| +1 | Beide Größen verhalten sich identisch – was bei der einen Größe vorne liegt, muss auch bei der anderen Größe vorne liegen. |
| … | … |
| 0 | Die beiden Größen haben nichts miteinander zu tun. |
| … | … |
| -1 | Beide Größen verhalten sich entgegengesetzt – was bei der einen Größe vorne liegt, liegt bei der anderen Größe hinten. |
Rangkorrelation an einem Beispiel
Um den Rangkorrelationskoeffizienten ein wenig anschaulicher zu machen, ein Beispiel:
Angenommen, wir haben 20 Pokerspieler und wissen irgendwoher, wie gut sie spielen, so dass wir sie ihrer Spielstärke nach ordnen können. Auf Platz 1 stünde der beste Spieler und auf Platz 20 der schlechteste. Entsprechend ihres Ranges in dieser Spielstärkerangliste geben wir den Spielern eine Nummer von 1 bis 20.
Dann lassen wir diese 20 Spieler ein Turnier spielen und schauen uns an, wie sie in dem Turnier abgeschnitten haben. Zwischen dem Rang der Spielstärke der Spieler und dem im Turnier erzielten Rang lässt sich nun der Rangkorrelationskoeffizienten berechnen.
Das Abschneiden in so einem Turnier könnte etwa wie folgt aussehen.
| Platzierung im Turnier | Spieler | Spielstärkerang |
| 1 | Spieler 1 | 1 |
| 2 | Spieler 2 | 2 |
| 3 | Spieler 5 | 5 |
| 4 | Spieler 8 | 8 |
| 5 | Spieler 3 | 3 |
| 6 | Spieler 9 | 9 |
| 7 | Spieler 14 | 14 |
| 8 | Spieler 4 | 4 |
| 9 | Spieler 6 | 6 |
| 10 | Spieler 7 | 7 |
| 11 | Spieler 12 | 12 |
| 12 | Spieler 18 | 18 |
| 13 | Spieler 10 | 10 |
| 14 | Spieler 11 | 11 |
| 15 | Spieler 17 | 17 |
| 16 | Spieler 16 | 16 |
| 17 | Spieler 15 | 15 |
| 18 | Spieler 13 | 13 |
| 19 | Spieler 20 | 20 |
| 20 | Spieler 19 | 19 |
In diesem Beispielturnier hätten die Spieler größtenteils entsprechend ihres Spielstärkeranges im Turnier abgeschnitten. Auf Platz 1 und 2 landeten die beiden besten Spieler, auf Platz 3 der fünft-beste Spieler, auf Platz 4 der acht-beste Spieler und so weiter.
Zwischen der Platzierung im Turnier und dem Spielstärkerang kann man nun den Rangkorrelationskoeffizienten berechnen. In diesem Beispielturnier ergibt sich ein Rangkorrelationskoeffizient von 0,85, was eine starke Korrelation von Spielstärke-Rang und Abschneiden in dem Beispielturnier bedeutet.
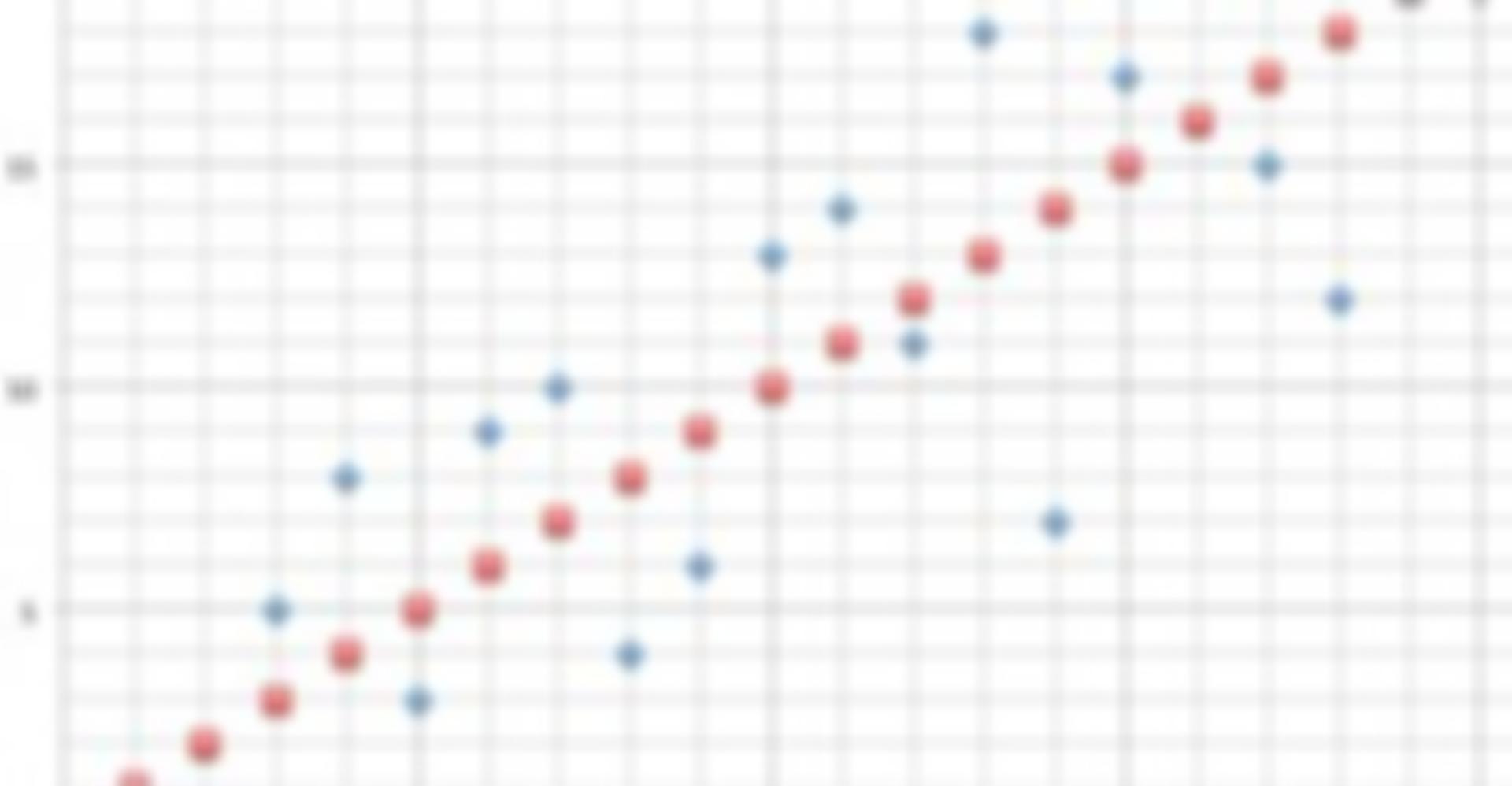
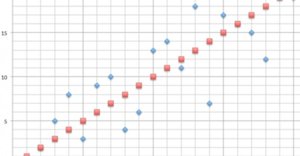
Graphisch kann man dieses Beispiel wie folgt darstellen: Auf der X-Achse sind die Spieler angegeben, auf der Y-Achse die Platzierung in dem Turnier. Die blauen Punkte entsprechen den Ergebnissen des Beispielturniers. Die roten Punkte zeigen an, wie die Spieler entsprechend ihres Spielstärkeranges abgeschnitten hätten.
Ein anderes Beispielturnier könnte dieses Ergebnis produzieren:
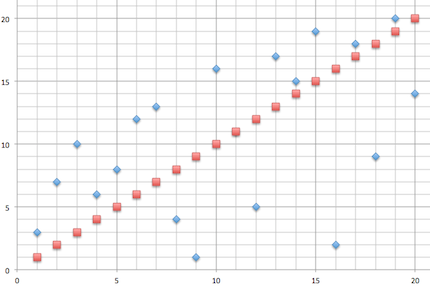
Die Ergebnisse der Spieler in diesem Beispielturnier weichen teilweise deutlich von ihrem Spielstärkerang ab, aber dennoch zeigt sich eine gewisse Korrelation von den beiden Größen.
Ein drittes Beispielturnier soll ein Bild von einem fast unkorrelierten Ergebnis zeigen:
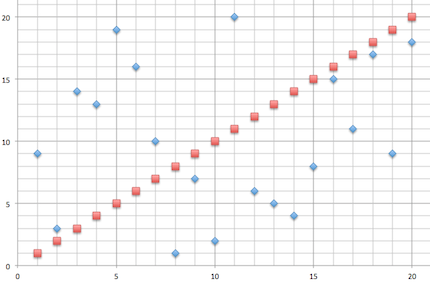
Ein Rangkorrelationskoeffizient von 0,13 deutet darauf hin, dass das tatsächliche Abschneiden der Spieler in dem Beispielturnier fast nichts mehr mit deren Spielstärke zu tun hat. Die Verteilung auf den einzelnen Plätzen ist fast zufällig.
Rangkorrelationskoeffizient und Glück versus Skill
Kann man bei Spielen oder Sportveranstaltungen, bei denen das Ergebnis am Ende in Form einer Tabelle vorliegt, den einzelnen Spielern oder Mannschaften einen Spielstärkerang zuordnen, ist es möglich den Spielstärkerang und die Platzierung in dem Spiel zu korrelieren.
Dieser so gewonnene Rangkorrelationskoeffizient ist ein starker Indikator dafür, welche Rolle Glück bei dem Spiel einnimmt.
Ein Rangkorrelationskoeffizient in der Nähe von 1 bedeutet, dass die Spieler größtenteils entsprechend ihrer Spielstärke abschneiden. Dies deutet darauf hin, dass Glück bei dem Spiel keine tragende Rolle spielt.
Ein Rangkorrelationskoeffizient in der Nähe von 0 bedeutet, dass die Ergebnisse der Spieler größtenteils unabhängig von ihrer Spielstärke sind. Dies deutet darauf hin, dass Glück die zentrale Rolle bei den Ergebnissen spielt.
Im Folgenden will ich mir zunächst Schach- und Fußball-Turniere ansehen und im Anschluss diese Betrachtungen auf Pokerturniere übertragen.
Der Rangkorrelationskoeffizient bei Schachturnieren
Schauen wir uns jetzt den Rangkorrelationskoeffizienten einmal in der Praxis an. Zunächst betrachte ich Schachturniere.
Die Teilnehmer eines Schachturniers lassen sich im Vorfeld anhand ihrer ELO-Zahl direkt nach ihrer Spielstärke sortieren.
Nach Abschluss des Turniers liegt für das Turnier eine Rangliste aller Spieler vor.
Der Rangkorrelationskoeffizient von dem Spielstärkerang der Schachspieler und dem tatsächlichen Ergebnis liegt bei den meisten Schachturnieren bei rund 0,9.
Das bedeutet, dass bei Schachturnieren die tatsächlichen Ergebnisse der Spieler sehr stark mit ihrer Spielstärke korreliert sind. Man kann also aus der bisher gemessenen Spielstärke der Schachspieler vergleichsweise verlässlich auf das Abschneiden in einem einzelnen Schachturnier schließen.
Dies deckt sich damit, dass Schachspiel ein Geschicklichkeitsspiel ist, bei dem Glück eine zu vernachlässigende Rolle spielt.
Der Rangkorrelationskoeffizient bei Fußballturnieren
Nehmen wir als nächstes Beispiel Fußballturniere – konkret die Fußballweltmeisterschaften 2002, 2006 und 2010.
Hier kann man den Mannschaften über die FIFA-Weltrangliste vor dem jeweiligen Turnier einen Spielstärkerang zuordnen. Die FIFA-Rangliste mag zwar nicht perfekt sein, um die tatsächliche Spielstärke einer Mannschaft zu ermitteln, ist aber hinreichend, da der Rangkorrelationskoeffizient gegenüber kleineren Ungenauigkeiten recht robust ist.
Für jedes der Weltmeisterschaftsturniere kann man eine Rangliste der 32 Mannschaften erstellen, welche ihr Abschneiden über alle Spiele widerspiegelt.
So kann man die Spielstärkeränge und die tatsächlich erzielten Ränge in den Turnieren miteinander korrelieren.
Nehmen wir zunächst die Fußball-WM 2010. Folgende Tabelle gibt das Abschneiden der einzelnen Länder und den Spielstärkerang nach FIFA-Weltrangliste 2010 wieder:
| Position | Land | Spielstärkerang | Position | Land | Spielstärkerang | |
| 1 | Spain | 2 | 17 | Côte d’Ivoire | 16 | |
| 2 | Netherlands | 3 | 18 | Slovenia | 29 | |
| 3 | Germany | 5 | 19 | Switzerland | 11 | |
| 4 | Uruguay | 20 | 20 | South Africa | 31 | |
| 5 | Argentina | 6 | 21 | Australia | 19 | |
| 6 | Brazil | 1 | 22 | New Zealand | 30 | |
| 7 | Ghana | 26 | 23 | Serbia | 17 | |
| 8 | Paraguay | 18 | 24 | Denmark | 21 | |
| 9 | Japan | 27 | 25 | Greece | 13 | |
| 10 | Chile | 14 | 26 | Italy | 4 | |
| 11 | Portugal | 9 | 27 | Nigeria | 23 | |
| 12 | United States | 10 | 28 | Algeria | 22 | |
| 13 | England | 7 | 29 | France | 8 | |
| 14 | Mexico | 15 | 30 | Honduras | 25 | |
| 15 | South Korea | 28 | 31 | Cameroon | 12 | |
| 16 | Slovakia | 24 | 32 | North Korea | 32 |
Ergebnis Fußball-WM 2010
Der berechnete Rangkorrelationskeoffizient zwischen Platzierung im Turnier und Spielstärkerang liegt für dieses Turnier bei 0,40.
Fußballweltmeisterschaft 2010: Rangkorrelationskoeffizient von 0,40
Graphisch stellen sich diese Ergebnisse wie folgt dar. Auf der X-Achse ist der Spielstärkerang und auf der Y-Achse die Platzierung im Turnier verzeichnet. Die einzelnen Länder sind als rote Punkte entsprechend ihrer Ränge eingetragen.
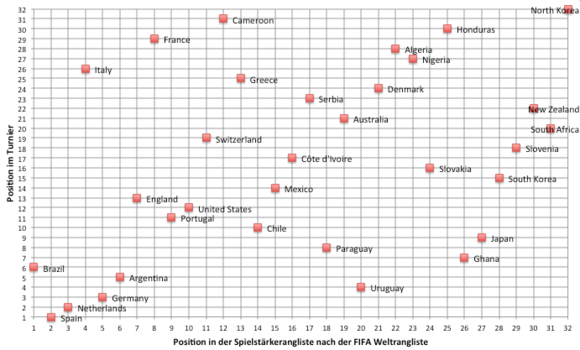
Fußballweltmeisterschaft 2006: Rangkorrelationskoeffizient von 0,47
Für die WM 2006 sieht das Diagramm wie folgt aus:
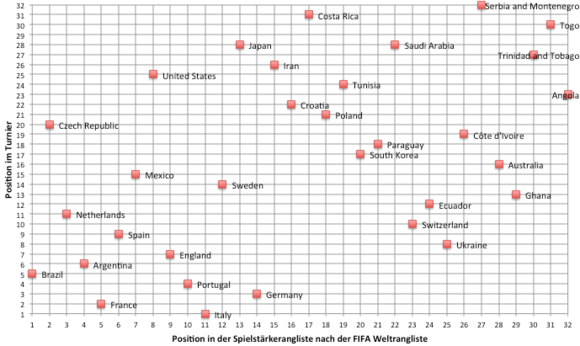
Fußballweltmeisterschaft 2002: Rangkorrelationskoeffizient von 0,28
Und dies ist das Diagramm für die WM 2002:
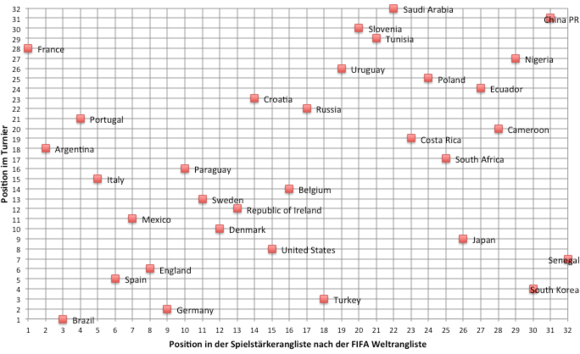
Dies sind die Rangkorrelationskoeffizienten zwischen Spielstärkerang und Platzierung für die Weltmeisterschaften 2002 bis 2010:
| Jahr | Rangkorrelationskoeffizient |
| 2002 | 0,28 |
| 2006 | 0,47 |
| 2010 | 0,40 |
| Mittel | 0,38 |
Die Rangkorrelationskoeffizienten bei den Turnieren von 2002 bis 2010 liegen zwischen 0,28 und 0,47 oder im Mittel bei 0,38.
Das heißt, für diese Turniere kann nur noch bedingt von dem über die FIFA-Weltrangliste berechneten Spielstärkerang der Mannschaften auf das tatsächliche Abschneiden in den Turnieren geschossen werden.
Herausragend ist hierbei insbesondere die WM 2002, wo viele Favoriten (Frankreich, Portugal, Argentinien) bereits in der Vorrunde scheiterten und sehr schwach eingeschätzte Mannschaften (Türkei, Südkorea) unter die letzten Vier kamen.
Diese Rangkorrelationskoeffizienten legen für Fußballturniere in Bezug auf die Frage nach Glücks- und Geschicklichkeitsanteil folgende Vermutung nahe: Fußballturniere haben einen signifikanten Glücksfaktor, so dass Vorhersagen über das Abschneiden einzelner Mannschaften nur sehr bedingt und mit einem großen Unsicherheitsfaktor möglich sind.
Dass bei Fußballspielen Glück eine Rolle spielt, hätte man auch schon vorher wissen können. Aber über den Rangkorrelationskoeffizienten lässt sich dieses Verhältnis quantifizieren und ebnet folgender Frage den Raum: Lassen sich Fußballturniere hinsichtlich ihres Glücks-Faktors mit Pokerturnieren vergleichen?
Der Rangkorrelationskoeffizient bei Pokerturnieren
Versucht man nun die Methode des Berechnens eines Rangkorrelationskoeffizienten auf Pokerturniere auszuweiten, stößt man leider sehr schnell an Grenzen. Während bei den meisten Turnieren anderer Sportarten akkurate Ranglisten geführt werden und Ergebnisse einzelner Spieler öffentlich verfügbar sind, gibt es für Pokerturniere kaum entsprechende Daten.
Ranglisten die von Hendon Mob, dem Bluff Magazin oder GPI erhoben werden, sind nur bedingt aussagekräftig über die Spielstärke der einzelnen Spieler, da ausschließlich positive Ergebnisse berücksichtigt werden und Ergebnisslisten von Pokerturnieren umfassen fast immer nur die Spieler, welche in den Geldrängen abgeschnitten haben.
Online sieht die Datenlage ein wenig besser aus, da hier zumindest akkurate Ergebnislisten geführt werden, welche allerdings auch nicht ohne weiteres öffentlich verfügbar sind.
Um eine Beispielrechnung für den Rangkorrelationskoeffizient bei Pokerturnieren durchführen zu können, habe ich auf die Ergebnisse der PokerOlymp Online Liga zurückgegriffen. Von diesen Turnieren stehen sämtliche Daten zur Verfügung und man kann auch eine Spielstärkerangliste für die einzelnen Teilnehmer angeben, indem man das Abschneiden über alle ausgetragenen Turniere berücksichtigt und dabei auch negative Ergebnisse einfließen lassen.
Ich habe insgesamt 63 Turniere aus dem Jahr 2012 betrachtet. Die Turniere hatten jeweils zwischen 25 und 45 Teilnehmern und insgesamt haben etwas über 200 verschiedene Spieler teilgenommen.
Basierend auf der Platzierung in einem Turnier habe ich jedem Spieler nach einer Formel, die negative Ergebnisse (außerhalb der Geldränge) berücksichtigt, Punkte gegeben1 und konnte so eine Spielstärkenrangliste über alle ausgetragenen Turniere gewinnen.
Wie aussagekräftig eine so gewonnene Spielstärkenrangliste hinsichtlich der Qualität der Spieler tatsächlich ist, soll für die weitere Betrachtung keine Rolle spielen, denn es geht bei der Untersuchung in erster Linie um die Frage, ob die Ergebnisse bisheriger Turniere mit den Ergebnissen eines Einzelturniers korrelieren.
Für jedes einzelne Turniere liegen die Platzierungen der teilnehmenden Spieler vor und diese lassen sich mit der Spielstärkerangliste der teilnehmenden Spieler korrelieren2.
Die Rangkorrelation einzelner Pokerturniere
Über die 63 Turniere ergaben sich sehr unterschiedliche Rangkorrelationskoeffizienten.
Die Berechnung der Rangkorrelationskoeffizienten erfolgte nach dem selben Prinzip wie bei den Fußball-Turnieren. Als Beispiel sei eines der 63 Turniere, Turnier Nummer 40, gegeben.
Das Ergebnis des Turniers ist in der folgenden Tabelle wiedergegeben. Angegeben sind neben der Platzierung auch die für dieses Turnier berechneten Punkte, sowie die Spielstärke (die Summe der berechneten Punkte des Spielers in allen anderen Turnieren) und der Spielstärkerang der teilnehmenden Spieler.
| Platz | Spieler | Punkte für dieses Turnier | Spielstärke | Spielstärkerang |
| 1 | vasa17 | 75,1 | 32,3 | 14 |
| 2 | dekalli | 54,9 | 41,7 | 12 |
| 3 | ralle1966 | 43,1 | 208,8 | 3 |
| 4 | strabjo | 34,7 | 21,8 | 17 |
| 5 | olgadnepr | 28,2 | 263,6 | 1 |
| 6 | kolja.ok | 22,9 | 154,7 | 6 |
| 7 | jewel213 | 18,4 | -88,1 | 27 |
| 8 | oobonsaioo | 14,5 | 28,3 | 15 |
| 9 | j.lupino | 11,1 | 209,4 | 2 |
| 10 | stine42 | 8,0 | 65,5 | 9 |
| 11 | axelrath | 5,2 | -167,0 | 28 |
| 12 | oqcpt | 2,7 | 9,0 | 19 |
| 13 | kamil147 | 0,4 | 56,5 | 10 |
| 14 | zottel1979 | -1,8 | 180,8 | 5 |
| 15 | terraluna74 | -3,8 | -78,4 | 25 |
| 16 | fighting25 | -5,7 | 104,1 | 7 |
| 17 | driese14 | -7,5 | -203,0 | 31 |
| 18 | terroraiser | -9,1 | 67,6 | 8 |
| 19 | awrati | -10,7 | -80,1 | 26 |
| 20 | rokechrv | -12,2 | -46,5 | 22 |
| 21 | 9hertz40 | -13,6 | 188,9 | 4 |
| 22 | ufimec5555 | -15,0 | -53,3 | 24 |
| 23 | aramson | -16,3 | -12,3 | 20 |
| 24 | andybes | -17,5 | 47,1 | 11 |
| 25 | ewelk | -18,7 | 10,8 | 18 |
| 26 | gahobre | -19,8 | -367,6 | 33 |
| 27 | aetiusxxx | -20,9 | -169,2 | 29 |
| 28 | priese | -22,0 | -218,3 | 32 |
| 29 | alecs_p06 | -23,0 | 27,9 | 16 |
| 30 | parademo | -24,0 | -47,4 | 23 |
| 31 | flo2608 | -25,0 | 37,2 | 13 |
| 32 | rheingauner | -25,9 | -183,9 | 30 |
| 33 | pokerlusche | -26,8 | -28,3 | 21 |
Tabelle eines der 63 untersuchten Turniere
Der Rangkorrelationskoeffizient zwischen Spielstärkerang und Platzierung im Turnier ergibt für dieses Turnier 0,47. Das Turnier hatte damit den höchsten Rangkorrelationskoeffizienten aller betrachteten Turnieren. Bei den meisten anderen Turnieren lag der Rangkorrelationskoeffizient deutlich niedriger oder im negativen Bereich.
Graphisch stellt sich dieses Turnier wie folgt dar. Wie bei den Diagrammen zu den Fußballweltmeisterschaften ist auf der X-Achse ist der Spielstärkerang und auf der Y-Achse die Platzierung im Turnier verzeichnet. Die einzelnen Spieler sind als rote Punkte entsprechend ihrer Ränge eingetragen.
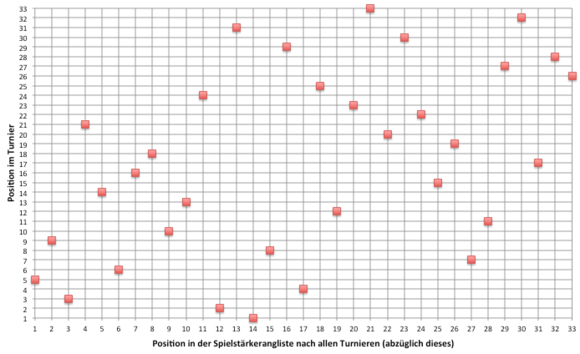
Aber viele andere Turniere hatten Rangkorrelationskoeffizienten wesentlich dichter an der Null, beziehungsweise sogar negative. In Turnieren mit einem negativen Rangkorrelationskoeffizienten schnitten die schlechteren Spieler besser ab als die besseren Spieler.
Hier der Graph eines der Turniere mit einem Rangkorrelationskoeffizienten von 0,01 – die Ergebnisse hier entsprechen einer fast völlig zufälligen Verteilung:
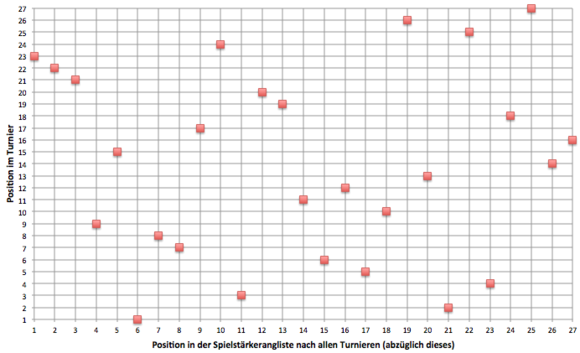
Die Rangkorrelationskoeffizienten für alle 63 betrachteten Turniere lagen zwischen -0,33 und +0,47. Dies sind alle Werte:
| 0,37 | 0,21 | 0,08 | -0,05 | 0,35 | 0,26 | 0,15 |
| 0,14 | -0,03 | -0,33 | 0,44 | 0,22 | -0,14 | -0,24 |
| 0,01 | 0,36 | -0,10 | 0,36 | 0,08 | -0,29 | -0,21 |
| 0,05 | 0,14 | 0,04 | 0,47 | 0,15 | 0,37 | 0,24 |
| 0,34 | 0,20 | 0,25 | -0,01 | -0,15 | -0,22 | -0,29 |
| 0,07 | 0,19 | -0,01 | -0,02 | -0,03 | -0,03 | -0,10 |
| 0,16 | 0,05 | 0,09 | 0,23 | -0,09 | 0,07 | 0,03 |
| 0,28 | 0,37 | 0,03 | -0,05 | 0,12 | 0,16 | 0,18 |
| -0,04 | 0,39 | 0,08 | 0,11 | 0,26 | 0,13 | 0,20 |
Der Mittelwert dieser 63 Rangkorrelationskoeffizienten liegt bei 0,1.
Mit anderen Worten: Die Ergebnisse eines einzelnen betrachteten Pokerturniers sind fast unkorreliert zu den Ergebnissen aller anderen Turniere. Die Spielstärke eines einzelnen Spielers (seine Ergebnisse über alle betrachteten Turniere) ist nur minimal mit den Ergebnissen eines einzelnen Turniers korreliert.
Das ist ein sehr starker Indikator dafür, dass die Ergebnisse einzelner Poker-Turniere einen exorbitanten Glücksfaktor haben.
Die Rangkorrelation mehrerer Turniere
Ein klein wenig anders wird das Bild, wenn man mehrere Turnierergebnisse zusammenfasst. Ich habe hierfür die 63 Turnier in zwei Untermengen geteilt – die Turniere mit einer geraden Nummer und die mit einer ungeraden. Dann ergab sich zwischen den Ergebnissen der geraden Turniere und den Ergebnissen der ungeraden Turniere ein Rangkorrelationskoeffizient von 0,14.
Sprich, über einen längeren Zeitraum korrelieren die Ergebnisse der einzelnen Spieler etwas stärker als über ein einzelnes Turnier. Aber von den Rangkorrelationskoeffizienten bei Fußball- oder Schachturnieren ist man immer noch sehr weit entfernt.
Das spricht dafür, dass der Glücksfaktor auch über eine größere Turnier-Menge den mit Abstand größten Einfluss auf die Ergebnisse der Spieler hat.
Anmerkungen zur Methode
Offensichtlich liefert die Methode der Rangkorrelation bei Pokerturnieren nur Ergebnisse, die den zugrundeliegenden Daten entsprechen. Es ist also durchaus möglich, dass der gefundene mittlere Rangkorrelationskoeffizient von 0,099 für einzelne Poker-Turniere eine Besonderheit der gewählten Datenmenge (der PokerOlymp Liga) ist.
Betrachtete man andere Turniere oder legte man einen wesentlich größeren Datenumfang zugrunde, dürften sich andere Zahlen zeigen. Aber es spricht sehr vieles dafür, dass auch bei anderen Poker-Turnieren der Rangkorrelationskoeffizient für einzelne Turniere in der Größenordnung von 0,1 liegt oder diese zumindest nicht deutlich übertrifft.
Betrachtete man Turniere mit mehr Teilnehmern, wird der Rangkorrelationskoeffizient tendenziell eher noch etwas niedriger anzusiedeln sein, insbesondere wenn viele Spieler nur wenige aller betrachteten Turniere spielen.
Die für in diesen Artikel geleistete Untersuchung verwendeten Daten greifen auf ein vergleichsweise geschlossenes Teilnehmer-Feld zurück. Spieler, die mindestens 50% der 63 betrachteten Turniere spielten, machten mit Abstand die meisten Datenpunkte aus, so dass die Spielstärkerangliste für diese Spieler eine aussagekräftige Relevanz hatte. Dies begünstigt eine stärkere Korrelation, so dass bei anderen Turnieren eher mit einem niedrigeren Rangkorrelationskoeffizienten für einzelne Turniere zu rechnen ist.
Bei Turnieren mit mehr Teilnehmern wäre mit einer höheren Fluktuation der Einzelteilnahmen zu rechnen und die daraus resultierende Spielstärkerangliste wäre weniger deutlich, wodurch die Rangkorrelation von Spielstärkerangliste und Ergebnis eines einzelnen Turniers notwendig niedriger ausfiele.
Die gewählte Formel, Punkte für Ergebnisse zu verteilen, um daraus eine Spielstärkerangliste zu errechnen, ist vergleichsweise flach und erlaubt für schlechte Platzierungen negative Punkte. Deswegen kann sie tatsächlich als ein Spielstärkeindikator gelten. Aber natürlich ist hier der Begriff “Spielstärke” in keiner Art und Weise absolut zu verstehen, sondern immer nur in dem Sinne, dass ein “spielstarker” Spieler nach dieser Formel besonders viele Punkte über alle betrachteten Turniere gesammelt hat und häufig Top-Platzierungen erreicht hat.
Man könnte anstelle der Formel auch einfach den Netto-Gewinn oder ROI eines Spielers wählen, um daraus die Spielstärke zu ermitteln. Doch da die Auszahlungen eines Poker-Turniers vergleichsweise steil sind und zum Beispiel keine Unterscheidung zwischen Platz 10 und Platz 35 in einem 40-Mann-Turnier machen (beide Spieler verlieren ihr Buy-In), wäre die daraus resultierende Spielstärke deutlich ungenauer und würde im Mittel zu einer niedrigeren Rangkorrelation zwischen der so ermittelten Spielstärke und den Einzelergebnissen führen.
Interpretation der Ergebnisse
Zunächst will ich nochmals das Ergebnis der Betrachtungen dieses Artikels festhalten. Folgende mittlere Rangkorrelationskoeffizienten wurden für einzelne Schach-, Fußball- und Pokerturniere gefunden:
| Spiel | Rangkorrelationskoeffizient |
| Schach | 0,9 |
| Fußball | 0,4 |
| Poker | 0,1 |
Ganz grob kann man die Interpretation dieses Ergebnisses mit einem Satz zusammenfassen: Glück spielt bei Schachturnieren fast keine Rolle, bei Fußballturnieren eine große Rolle und bei Pokerturnieren eine überragende Rolle.
Ein Pokerturnier ist deswegen aber keineswegs per se ein reines Glücksspiel. Die Argumentation aus einem meiner älteren Artikel hat weiterhin bestand: Poker hat eine ausgeprägte Geschicklichkeitskomponente, ist aber darauf ausgelegt, dass die konkreten Karten zufällig sind.
Allerdings spiegelt sich diese Geschicklichkeitskomponente statistisch nur minimal in den Ergebnissen eines einzelnen Turniers wider. Bei einem einzelnen Turnier würde man aus statistischer Sicht wenig falsch machen, wenn man die Ergebnisse als praktisch völlig zufällig interpretierte.
Auch zeigt sich, dass die Betrachtung mehrerer zusammengefasster Turnierergebnisse noch keine deutliche Korrelation zwischen Spielstärke (basierend auf allen Ergebnissen) und tatsächlichem Abschneiden in mehreren Einzelturnieren erkennen lässt. Einfach gesagt: Auch nach zig Turnieren sind die Ergebnisse einzelner Spieler größtenteils unabhängig von ihrer Spielstärke.
Andererseits legt die Untersuchung nahe, dass es vernünftig ist, davon auszugehen, dass der Rangkorrelationskoeffizient zwischen zusammengefassten Ergebnissen mehrerer Turniere und der Spielstärkerangliste mit der Anzahl der betrachteten Turniere steigt. Sprich: Je mehr Turniere man betrachtet, desto mehr korrelieren die Ergebnisse mit der Spielstärke.
Allerdings scheint sich eine stärkere Korrelation nur sehr langsam zu zeigen. In der für diesen Artikel genutzten Datenmenge ergab sich für Einzelturniere eine Rangkorrelation von 0,099 und für die Zusammenfassung von etwas über 30 Turnieren eine Rangkorrelation von 0,14.
Dabei muss nochmals darauf hingewiesen werden, das die hier untersuchten Turniere allesamt weniger als 50 Teilnehmer hatten. Betrachtete man Turniere mit mehr Teilnehmern zeigten sich fast sicher noch niedrigere Korrelationskoeffizienten.
Überträgt man diese statistischen Ergebnisse auf das Live-Poker-Geschehen, kann man festhalten, dass die Turnierergebnisse einzelner Spieler auch über den Zeitraum eines Jahres zusammengefasst größtenteils zufällig und glücksabhängig sind. Es dürfte mehrerer hundert, wenn nicht gar tausender Turniere benötigen, um eine Fußballturnier-ähnliche Korrelation zwischen Spielstärke und tatsächlichen Ergebnissen zu erhalten.
1 Die Formel sie wie folgt aus:
( LOG2 ( S / P ) * F2 / ( F2 / LN(2) – 0,5 * LOG2 ( S * 2 * π ) ) – 1 ) * ( 1 + LOG2 ( B + 1 ) ) * 10
S: Anzahl der Mitspieler, P: Platzierung des Spielers im Turnier, B: Buy-In
Bei dieser Formel sind negative Punkte möglich und für ein einzelnes Turnier ergibt die Summe der Punkte aller Spieler immer genau Null.
2 Ich habe die Spielstärkerangliste jeweils über alle 63 Turniere abzüglich des jeweils betrachteten Turniers berechnet. Das heißt alle erst zu einem späteren Zeitpunkt gespielte Turniere wurden auch für die Spielstärkerangliste berücksichtigt, aber – und das ist wichtig, da es sonst die Messgröße verzerren würde – das jeweils betrachtete Turnier nicht.
Dieser Artikel erschien auf PokerOlymp am 11.04.2016.