Wer eins-null führt, der stets verliert und der Chipleader von Tag 1 schafft es nie ins Geld – ist an diesen häufig geäußerten Gemeinplätzen irgendwas dran?
“In 95% der Fälle gibt einem (ein früher großer Stack) kaum Vorteile im weiteren Turnierverlauf”, schrieb heute einer unserer Kommentatoren unter dem jüngst hier veröffentlichten Artikel von Lee Davy. Der Frage, was so eine frühe Führung wert ist, bin ich einmal mathematisch auf den Grund gegangen.
Dafür schaute ich mir die jüngsten 5 EPT-Turniere (Deauville, Berlin, London, Monte Carlo und Barcelona) an und verglich die finalen Ergebnisse aller Spieler mit deren Abschneiden nach dem jeweiligen Tag 1.
Ergebnisse
Ich nehme die konkreten Ergebnisse vorweg: Eine frühe Führung ist enorm viel Wert. Wer den ersten Tag in der oberen Hälfte des Chipcounts abschneidet, gewinnt im Schnitt 4 Mal so viel Geld, kommt 5 Mal häufiger an den Final-Table und 2,5 Mal häufiger ITM, als jemand, der den ersten Tag in der unteren Hälfte des Chipcounts beendet.
Ferner besteht zwischen dem Rang nach Tag 1 und dem finalen Rang ein Korrelationskoeffizient von 51% – sprich, ganz grob gesprochen, die Spieler beenden ein Turnier bis zu einem gewissen Grad (eben 51%) genauso, wie sie Tag 1 beendeten.
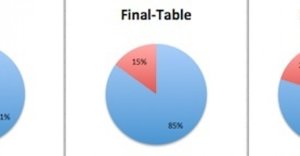
In Torten-Diagrammen sieht dies wie folgt aus:
Diese Zahlen werden etwas weiter unten noch detaillierter betrachtet.
Q nach Tag 1 und Abschneiden im Turnier
Für die weiteren Untersuchungen reihte ich die Spieler entsprechend ihrem Q nach Tag 1 auf. Q gibt das Verhältnis des Stacks eines Spielers zum Durchschnittsstack an – hat ein Spieler zum Beispiel 100.000 Chips, während der Durchschnitt bei 50.000 Chips liegt, hat er ein Q von 2.
Spieler, die im Laufe eines Turniers vor den Geldrängen ausschieden, hatten nach Tag 1 im Schnitt ein Q von 0,87 – also weniger als Average. Die Spieler, die die Geldränge erreichten, hatten im Schnitt ein Q von 1,35. Spieler, die den Final-Table erreichten, hatten im Schnitt gar ein Q von 1,45 – fast anderthalbfachen Average nach Tag 1.
| Spielerkaterogie | Durchschnitts-Q nach Tag 1 |
| Bust vor der Bubble | 0,87 |
| ITM | 1,35 |
| Final-Table | 1,45 |
Stellt man das Abschneiden aller Spieler nach Tag 1 den erreichten Preisgeldern graphisch gegenüber ergibt sich folgendes Bild:
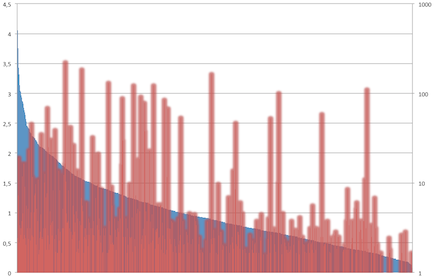
Die Spieler in obigem Diagramm sind entsprechend ihres Qs nach Tag 1 geordnet und ihre jeweils erreichten Preisgelder entsprechen den roten Balken.
Auf den ersten Blick, sieht es so aus, als hätte die blaue Fläche (die Qs) nicht so viel mit den roten Balken (den Preisgeldern) zu tun. Aber man sieht sehr schnell, dass auf der linken Seite des Diagramms (bei den hohen Qs nach Tag 1) wesentlich häufiger höhere Preisgelder erreicht wurden. Weiter rechts findet man deutlich weniger Top-Platzierungen mit hohen Preisgeldern.
Korrelationskoeffizienten
Die statistisch spannende Frage ist, wie die Korrelation zwischen dem Q eines Spielers nach Tag 1 und dem von ihm erspielten Preisgeld aussieht. Der Korrelationskoeffizient gibt Auskunft darüber, wie sehr zwei statistische Größen voneinander (linear) abhängen1.
Korreliert man das Q der Spieler nach Tag 1 mit ihrem erreichten Preisgeld, kommt man auf einen Korrelationskoeffizienten von 0,1 (oder 10%) – das entspricht einer eher geringen Korrelation.
Wesentlich spannender wird es jedoch, wenn man die Abschlussplatzierungen der Spieler mit den Platzierungen nach Tag 1 vergleicht. Dies macht man über den Rangkorrelationskoeffizienten2.
Hier ergeben sich bei den betrachteten 5 EPT-Turnieren Werte zwischen 23% und 39% – sprich, zwischen dem Rang nach Tag 1 und dem finalen Rang der einzelnen Spieler gibt es in jedem Turnier eine stärkere Korrelation.
| Turnier | Korrelation Q nach Tag 1 vs. Preisgeld | Korrelation Rang Tag 1 vs. finaler Rang |
| Deauville (Saison 9) | 6,6% | 32,2% |
| London (Saison 9) | 12,5% | 39,3% |
| Berlin (Saison 9) | 7,1% | 32,4% |
| Monte Carlo (Saison 9) | 10,9% | 23,3% |
| Barcelona (Saison 10) | 12,7% | 32,6% |
Noch deutlicher werden die Zahlen, wenn man alle 5 betrachteten Turniere zusammen analysiert. Dann ergibt sich zwischen dem Rang nach Tag 1 und finalen Rang ein Korrelationskoeffizient von 51%.
Turnier-Erwartungen in Abhängigkeit vom Tag-1-Ergebnis
Insgesamt hatte meine Stichprobe 2.208 Spieler nach Tag 1 mit Chips. Teilt man diese Spieler gleichmäßig in 10 Gruppen, sortiert nach dem Q nach Tag 1 auf, ergeben sich detaillierte Aussagen, die man über die Gewinn-Erwartungen in Abhängig vom Tag-1-Ergebnis treffen kann.
So schafften es zum Beispiel fast 63% aller Spieler, die Tag 1 in den Top-10-Prozent abschlossen (mit einem Q von über 1,88) am Ende ins Geld. Von den Bottom-10-Prozent aller Spieler nach Tag 1 schafften es grade mal 6,6% ins Geld.
| Q nach Tag 1 | ITM-Quote | Final-Table-Quote | Ø-Gewinn (Buy-Ins) |
| >1,88 | 62,7% | 4,5% | 3,3 |
| 1,45 – 1,88 | 42,3% | 3,2% | 3,7 |
| 1,22 – 1,45 | 36,8% | 2,7% | 2,9 |
| 1,03 – 1,22 | 35,6% | 4,1% | 3,5 |
| 0,88 – 1,03 | 20,5% | 0,9% | 1,4 |
| 0,74 – 0,88 | 20,1% | 0,9% | 0,8 |
| 0,61 – 0,74 | 19,4% | 0,9% | 1,1 |
| 0,47 – 0,61 | 18,3% | 0,5% | 0,7 |
| 0,33 – 0,47 | 15,4% | 0,5% | 1,0 |
| 0,00 – 0,33 | 6,6% | 0,0% | 0,2 |
Extreme Fälle in Stichprobe
Der Spieler, der es in den 5 betrachteten EPT-Turnieren mit den wenigsten Chips in Geld schaffte, war Amir Mansouri bei der EPT Berlin 2013. Nach Tag 1 hatte er grade mal 6.600 Chips (22% des Startstacks bei einem Durchschnittsstack von etwa 55.000). Am Ende erspielte er sich 8.000 Euro.
Ebenfalls in Berlin schaffte Robert Haigh das Kunststück, den zweiten Platz zu erreichen, obwohl er nach Tag 1 nur 19.800 Chips (unter Startstack, Q von etwa 0,35) hatte.
Nochmals Berlin: Mike Kunze war nach Tag 1 Zweiter in Chips mit 188.000 Chips (mehr als 6-facher Startstack und ein Q von 3,3), schaffte es aber dennoch nicht ins Geld.
Methode
Von den 5 jüngsten EPTs (Deauville, London – März 2013, Berlin, Monte Carlo, Barcelona) habe ich die jeweiligen Chipcounts von Tag 1 genommen und den finalen Platzierungen und Preisgelder gegenübergestellt. Die Turniere haben allesamt den selben Startstack und eine sehr ähnliche Blind- und Auszahlungstruktur, weswegen sie sich für einen Vergleich anbieten.
Für die Rangkorrelationen wurde allen Spielern, die es nicht ins Geld schafften der erste Nicht-Preisgeld-Rang gegeben – waren also 100 Spieler ITM, wurde allen Spieler, die vor dem Geld ausschieden, Rang 101 zugeteilt.
Insgesamt liegen der Stichprobe 2.208 Datenpunkte (Spieler mit Chips nach dem jeweiligen Tag-1) zugrunde. Für jedes einzelne Turnier habe ich dabei den Q (Verhältnis vom Stack eines Spielers zum Durchschnittsstack) eines jeden Spielers nach Tag 1 berechnet, sowie seinen Gewinn-Anteil vom Gesamtpreisgeld berechnet. Durch Letzteres wurde für den Gesamt-Vergleich herausgerechnet, dass die Turniere unterschiedliche Buy-Ins hatten.
1 Generell ist ein Korrelationskoeffizient ist ein Maß in der Statistik, welches – vereinfacht gesprochen – angibt, wie stark zwei Messgrößen voneinander abhängen. Er nimmt Werte zwischen -1 und +1 an.
Ein Korrelationskoeffizient von +1 entspricht einer direkten proportionalen Korrelation. Wenn sich zum Beispiel die eine Messgröße verdoppelt, muss sich auch die andere verdoppeln.
Ein Korrelationskoeffizient von -1 entspricht einem antiproportionalen Verhältnis – verdoppelt sich die eine Größe, halbiert sich die andere.
Ein Korrelationskoeffizient von 0 sagt aus, dass die beiden Messgrößen statistisch gar nicht korrelieren, das heißt, dass vom Verhalten der einen Größe keine Rückschlüsse auf das Verhalten der anderen Größe gezogen werden können.
2 Der Rangkorrelationskoeffizient ist eine spezielle Form des Korrelationskoeffizienten, der nicht die Messgrößen selbst vergleicht, sondern die Ränge, welche die einzelnen Werte der beiden Reihen einnehmen.
Ganz einfach formuliert, haben verschiedene Rangkorrelationskoeffizienten zwischen zwei Messgrößen folgende Bedeutungen.
| Rangkorrelationskoeffizient | Bedeutung |
| +1 | Beide Größen verhalten sich identisch – was bei der einen Größe vorne liegt, muss auch bei der anderen Größe vorne liegen. |
| … | … |
| 0 | Die beiden Größen haben nichts miteinander zu tun. |
| … | … |
| -1 | Beide Größen verhalten sich entgegengesetzt – was bei der einen Größe vorne liegt, liegt bei der anderen Größe hinten. |
Dieser Artikel erschien auf PokerOlymp am 11.04.2016.