Das Gesetz der großen Zahlen ist eines der bekanntesten Gesetze der Wahrscheinlichkeitsrechnung und hat in unserer Serie der wunderlichen Welt der Wahrscheinlichkeiten auch seinen Platz verdient. In diesem Artikel soll dieses Gesetz anschaulich erläutert werden und am Ende wollen wir aufzeigen, was das Ganze mit Poker zu tun hat.
Was besagt das Gesetz der Gesetz der großen Zahlen?
Ganz profan gesprochen, besagt das Gesetz der großen Zahlen, dass die relative Häufigkeit eines zufälligen Ereignisses um die Wahrscheinlichkeit des Ereignisses herum liegt. Ein Beispiel macht das deutlicher: Ich werfe eine Münze 100 Mal, dann darf ich erwarten, dass mehr oder weniger 50 Mal Kopf fällt, denn die Wahrscheinlichkeit, dass bei einem Wurf Kopf fällt, liegt bei 50 Prozent.
Das klingt erst einmal sehr plausibel und die Gültigkeit dieses Gesetzes war schon mit dem Aufkommen der Wahrscheinlichkeitsrechnung vermutet worden. Aber ein rigoroser mathematischer Beweis folgte erst wesentlich später. In der Stochastik ist das Gesetz ein elementarer Grundstein für unzählige andere Theoreme und Anwendungen und auch für Pokerspieler ist das Gesetz nützlich. Schauen wir es uns anhand eines einfachen Beispiels genauer an:
Münzwurf-Beispiel
Nehmen wir zur Veranschaulichung des Gesetzes der großen Zahlen abermals den Münzwurf.
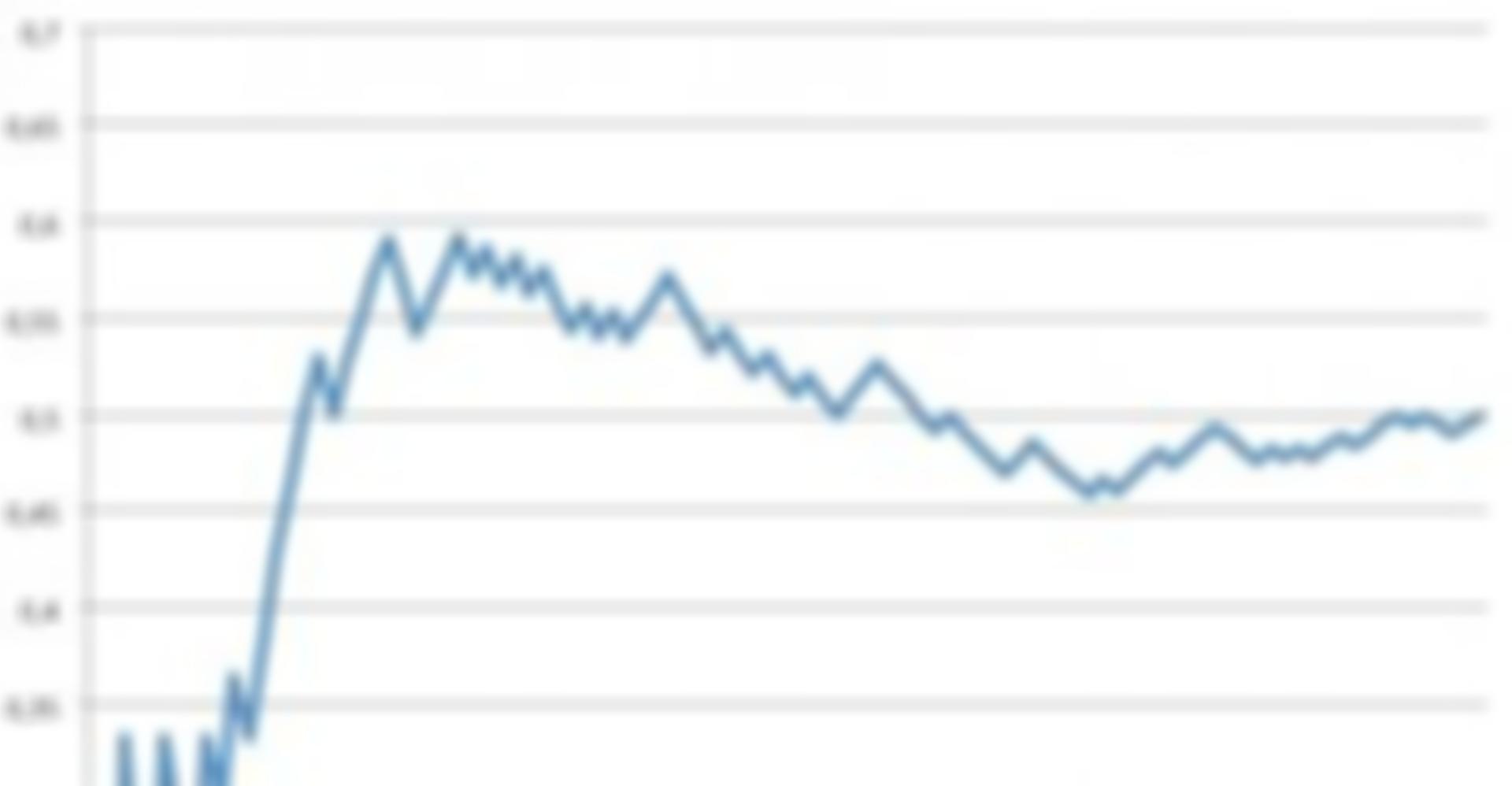
Wenn wir 100 Mal eine Münze werfen und nach jeden Wurf die relative Häufigkeit des Ereignisses “Kopf” notieren, könnte folgendes Diagramm herauskommen:
Das Gesetz der großen Zahl besagt nun, dass sich die blaue Linie in diesem Diagramm immer weiter der 0,5 (das heißt 50 Prozent) annähern wird, je mehr Münzwürfe wir durchführen.
Was das Gesetz der großen Zahl nicht aussagt
Es ist nun allerdings nicht so, dass in dem Beispiel des Münzwurfes die relative Häufigkeit auf lange Sicht genau 50 Prozent beträgt. Tatsächlich ist diese Wahrscheinlich sehr gering und bei genügend Wiederholungen ziemlich dicht an der Null dran. Die Wahrscheinlichkeit bei 100 Münzwürfen genau 50 Mal Kopf zu werfen liegt bei rund 8%, die Wahrscheinlichkeit bei 1.000 Würfen genau 500 Mal Kopf zu werfen schon nur noch 2,5%.
Eine genauere Betrachtung des Gesetzes
Die Häufigkeit liegt also nicht unbedingt bei genau 50 Prozent, wohl aber ziemlich dicht dran. Die Wahrscheinlichkeit, dass die relative Häufigkeit der Kopf-Würfe bei dem oben aufgeführten Beispiel um einen bestimmten Faktor von 50% abweicht, wird mit der Anzahl der Würfe immer geringer.
Was meint das? Betrachten wir zum Beispiel eine Abweichung um den Faktor 10 Prozent. Und nun fragen wir uns: Wie groß ist die Wahrscheinlichkeit, dass wir bei 100 Würfen 10 Prozent häufiger oder seltener Kopf werfen als die erwarteten 50 Mal. Sprich: Wie oft werfen wir weniger als 45 Mal oder häufiger als 55 Mal Kopf? Das kann man leicht (über die Binomialverteilung) ausrechnen: Die Wahrscheinlichkeit beträgt 27%.
Nun schauen wir uns das gleiche bei 1.000 Würfen an. Eine Abweichung vom Faktor 10% bedeutete hier weniger 450 Mal oder mehr als 550 Mal Kopf. Die Wahrscheinlichkeit, dass so ein Ereignis eintritt, liegt nur noch bei 0,14%. Das ist reichlich unwahrscheinlich und je mehr Würfe wir durchführen, desto unwahrscheinlicher wird eine solche Abweichung.
Was das Gesetz der großen Zahlen nun aussagt, ist, dass diese Wahrscheinlichkeit – völlig egal, welche Abweichung man wählt – mit genügend Wiederholungen immer gegen Null geht.
Betrachten wir eine Abweichung vom Faktor 2 Prozent. Bei 100 Würfen hieße dies weniger als 49 Mal oder mehr mehr als 51 Mal Kopf. Die Wahrscheinlichkeit hierfür beträgt 76 Prozent . Bei 1.000 Würfen liegt die Wahrscheinlichkeit für eine solche Abweichung (weniger als 490 Mal oder mehr als 510 Mal Kopf) schon nur noch bei 51 Prozent und bei 10.000 Würfen (weniger als 4900 Mal oder mehr als 5100 Mal Kopf) nur noch bei 4 Prozent.
Auch wenn man eine Abweichung von nur 1 oder 0,1 Prozent wählt – die Wahrscheinlichkeit, dass die relative Häufigkeit so weit vom Erwartungswert abweicht, wird immer gegen Null gehen, wenn man das zufällige Ereignis nur genügend oft wiederholt. Genau das ist das Gesetz der großen Zahlen.
Wenn dreimal rot kommt, wird schwarz wahrscheinlicher

Ein Irrglaube ist es, dass das Gesetz der großen Zahlen einen Einfluss der Natur hat, dass es zu selten eingetretene Ereignisse irgendwie wahrscheinlicher macht, damit das Mittel am Ende stimmt.
Dem ist nicht so. Die Wahrscheinlichkeit, dass beim Münzwurf Kopf fällt, beträgt immer 50 Prozent. Die Wahrscheinlichkeit, dass beim (europäischen) Roulette rot kommt, beträgt immer 48,6 Prozent, egal wie häufig vorher rot kam. Scheinbar merkwürdige Abweichungen kommen bei wenigen Wiederholungen ständig vor, haben aber keinen Einfluss auf das Gesetz der großen Zahl.
Betrachtet man 10.000 Münzwürfe, ist es für die relative Häufigkeit von Kopf oder Zahl ziemlich egal, was während der ersten 5 Würfe passiert ist. Fünf Mal Kopf macht bei so vielen Würfen auch nur eine Abweichung von 0,05 Prozent aus. Und ebenso gut kann (und wird) es passieren, dass während der 10.000 Würfe dann und wann auch 5 Mal Zahl kommt.
Das Gesetz der großen Zahl sagt eben nicht aus, dass sich Kopf und Zahl oder Rot und Schwarz genau ausgleichen werden, sondern nur dass ihre relativen Häufigkeiten auf lange Sicht entsprechend ihrer Wahrscheinlichkeiten eintreten werden. Nicht ganz genau, aber beliebig genau, wenn man nur genügend Wiederholungen des Münzwurfes oder Roulettespiels durchführt.
Das Gesetz der großen Zahlen und Poker?
Und was hat das Ganze nun mit Poker zu tun? Zugegeben, die Verbindungen zwischen dem Gesetz der großen Zahl und Poker sind vor allem theoretischer Natur und die alleinige Kenntnis dieses Gesetzes wird wohl kaum einen zu einem besseren Spieler machen.
Aber Poker und die Verteilungen der Karten hängen am Ende komplett am Gesetz der großen Zahl.
Nehmen wir zum Beispiel Asse beim Texas Hold’em. Statistisch bekommt man alle 221 Hände einmal Asse als Startkarten. Das heißt nicht, dass man genau alle 221 Hände Asse bekommt, sondern dass die relative Häufigkeit bei eins zu 221 liegt. Es kann passieren, dass man über 1.000 Hände gar keine Asse bekommt (die Wahrscheinlichkeit hierfür liegt bei etwas über einem Prozent), aber über einen hinreichend großen Zeitraum werden ziemlich genau 0,45 Prozent aller Hände (das entspricht einer von 221) Asse sein.
Die Wahrscheinlichkeit, dass die relative Häufigkeit mehr als 10 Prozent davon abweicht, nimmt mit zunehmender Anzahl von Händen drastisch ab.
Wir haben diese Wahrscheinlichkeit einmal für bis zu 200.000 Hände ausgerechnet:
| Anzahl Hände | Erwartete Häufigkeit für Asse | 10% Abweichung | Wahrscheinlichkeit für größere Abweichung |
| 1.000 | 4,5 | 4 – 5 | 67% |
| 10.000 | 45 | 41 – 50 | 48% |
| 100.000 | 452 | 407 – 498 | 3% |
| 200.000 | 905 | 814 – 995 | 0,2% |
Bei vergleichsweise wenigen Händen ist noch recht wahrscheinlich, dass man etwas zu viele oder zu wenige Asse bekommt, aber je mehr Hände man spielt, desto sicherer ist es, dass die Anzahl der erhaltenen Asse ziemlich dicht am Erwartungswert dran ist.
Und das gilt natürlich nicht nur für Asse, sondern für praktisch alles, was beim Poker passieren kann: Sets treffen, Draws treffen oder verpassen, Flips gewinnen, mit Königen in Asse laufen und so weiter.
Am Ende passiert auf lange Sicht alles in etwa mit der Frequenz, die der Wahrscheinlichkeit des Einzelereignisses entspricht. Das stellt das Gesetz der großen Zahlen sicher. Das heißt nicht, dass alles immer genau mit der entsprechenden Frequenz eintritt – man kann auch dreimal hintereinander Asse bekommen oder zehn Flushdraws in Folge verpassen, aber wenn man genügend Hände spielt, wird es äußerst wahrscheinlich, dass man sehr nah am Erwartungswert dran ist. Und das hat doch irgendwie etwas Beruhigendes.
Dieser Artikel erschien auf PokerOlymp am 11.04.2016.